Green’s Function and TD-DMRG
[1]:
!pip install block2==0.5.2rc13 -qq --progress-bar off --extra-index-url=https://block-hczhai.github.io/block2-preview/pypi/
!pip install pyscf==2.3.0 -qq --progress-bar off
In the following example, we calculate the electron removal (IP) part of one-particle Green’s function for Hydrogen chain (\(\mathrm{H_6}\)) in the minimal basis:
where \(|\Psi_0\rangle\) is the ground state, \(i = j = 2\) (counting from zero), \(\eta = 0.005\).
The Green’s function can be computed using DMRG in either the frequency domain (dynamical DMRG) or the time domain (time-dependent DMRG).
Dynamical DMRG
We first solve the response equation to find the Green’s function in the frequency domain.
Note that the return value of driver.greens_function method is the state:
Therefore, to get the value for Green’s function with \(i\neq j\), one can simply use driver.expectation to compute the dot product of \(|X_i\rangle\) with some other \(a_j|\Psi_0\rangle\).
In the SU2 mode:
[2]:
import numpy as np
from pyblock2._pyscf.ao2mo import integrals as itg
from pyblock2.driver.core import DMRGDriver, SymmetryTypes
from pyscf import gto, scf, lo
BOHR = 0.52917721092
R = 1.8 * BOHR
N = 6
mol = gto.M(atom=[['H', (i * R, 0, 0)] for i in range(N)], basis="sto6g", symmetry="c1", verbose=0)
mf = scf.RHF(mol).run(conv_tol=1E-14)
mf.mo_coeff = lo.orth.lowdin(mol.intor('cint1e_ovlp_sph'))
ncas, n_elec, spin, ecore, h1e, g2e, orb_sym = itg.get_rhf_integrals(mf, ncore=0, ncas=None, g2e_symm=8)
driver = DMRGDriver(scratch="./tmp", symm_type=SymmetryTypes.SU2, n_threads=4)
driver.initialize_system(n_sites=ncas, n_elec=n_elec, spin=spin, orb_sym=orb_sym)
bond_dims = [150] * 4 + [200] * 4
noises = [1e-4] * 4 + [1e-5] * 4 + [0]
thrds = [1e-10] * 8
mpo = driver.get_qc_mpo(h1e=h1e, g2e=g2e, ecore=ecore, integral_cutoff=1E-8, iprint=1)
ket = driver.get_random_mps(tag="KET", bond_dim=150, nroots=1)
energy = driver.dmrg(mpo, ket, n_sweeps=20, bond_dims=bond_dims, noises=noises,
thrds=thrds, iprint=1)
print('Ground state energy = %20.15f' % energy)
isite = 2
mpo.const_e -= energy
eta = 0.005
dmpo = driver.get_site_mpo(op='D', site_index=isite, iprint=0)
dket = driver.get_random_mps(tag="DKET", bond_dim=200, center=ket.center, left_vacuum=dmpo.left_vacuum)
driver.multiply(dket, dmpo, ket, n_sweeps=10, bond_dims=[200], thrds=[1E-10] * 10, iprint=1)
freqs = np.arange(-0.8, -0.2, 0.01)
gfmat = np.zeros((len(freqs), ), dtype=complex)
for iw, freq in enumerate(freqs):
bra = driver.copy_mps(dket, tag="BRA") # initial guess
gfmat[iw] = driver.greens_function(bra, mpo, dmpo, ket, freq, eta, n_sweeps=6,
bra_bond_dims=[200], ket_bond_dims=[200], thrds=[1E-6] * 10, iprint=0)
print("FREQ = %8.2f GF[%d,%d] = %12.6f + %12.6f i" % (freq, isite, isite, gfmat[iw].real, gfmat[iw].imag))
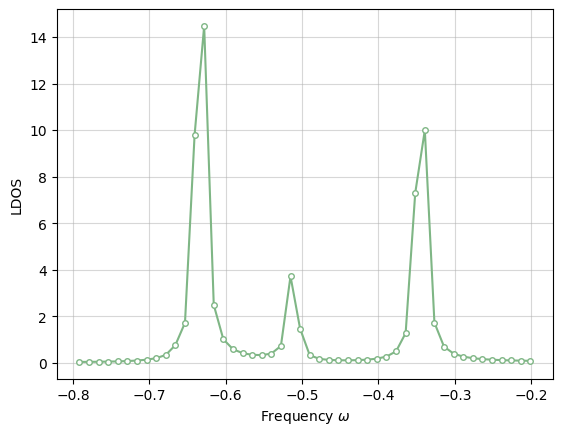
ldos = -1 / np.pi * gfmat.imag
import matplotlib.pyplot as plt
plt.grid(which='major', axis='both', alpha=0.5)
plt.plot(freqs, ldos, linestyle='-', marker='o', markersize=4, mfc='white', mec="#7FB685", color="#7FB685")
plt.xlabel("Frequency $\\omega$")
plt.ylabel("LDOS")
plt.show()
integral symmetrize error = 0.0
integral cutoff error = 0.0
mpo terms = 863
Build MPO | Nsites = 6 | Nterms = 863 | Algorithm = FastBIP | Cutoff = 1.00e-20
Site = 0 / 6 .. Mmpo = 13 DW = 0.00e+00 NNZ = 13 SPT = 0.0000 Tmvc = 0.000 T = 0.008
Site = 1 / 6 .. Mmpo = 34 DW = 0.00e+00 NNZ = 100 SPT = 0.7738 Tmvc = 0.000 T = 0.004
Site = 2 / 6 .. Mmpo = 56 DW = 0.00e+00 NNZ = 185 SPT = 0.9028 Tmvc = 0.000 T = 0.004
Site = 3 / 6 .. Mmpo = 34 DW = 0.00e+00 NNZ = 419 SPT = 0.7799 Tmvc = 0.001 T = 0.004
Site = 4 / 6 .. Mmpo = 14 DW = 0.00e+00 NNZ = 105 SPT = 0.7794 Tmvc = 0.000 T = 0.003
Site = 5 / 6 .. Mmpo = 1 DW = 0.00e+00 NNZ = 14 SPT = 0.0000 Tmvc = 0.000 T = 0.002
Ttotal = 0.027 Tmvc-total = 0.002 MPO bond dimension = 56 MaxDW = 0.00e+00
NNZ = 836 SIZE = 4753 SPT = 0.8241
Rank = 0 Ttotal = 0.057 MPO method = FastBipartite bond dimension = 56 NNZ = 836 SIZE = 4753 SPT = 0.8241
Sweep = 0 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.061 | E = -3.2667431000 | DW = 1.41e-20
Sweep = 1 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.105 | E = -3.2667431000 | DE = 7.11e-15 | DW = 9.98e-21
Sweep = 2 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.148 | E = -3.2667431000 | DE = 0.00e+00 | DW = 1.25e-20
Sweep = 3 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.197 | E = -3.2667431000 | DE = -1.78e-15 | DW = 1.88e-20
Sweep = 4 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.238 | E = -3.2667431000 | DE = 1.78e-15 | DW = 1.13e-20
Sweep = 5 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.280 | E = -3.2667431000 | DE = 1.78e-15 | DW = 1.19e-20
Sweep = 6 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.319 | E = -3.2667431000 | DE = -1.78e-15 | DW = 9.42e-21
Sweep = 7 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.365 | E = -3.2667431000 | DE = -1.78e-15 | DW = 2.01e-20
Sweep = 8 | Direction = forward | Bond dimension = 200 | Noise = 0.00e+00 | Dav threshold = 1.00e-09
Time elapsed = 0.400 | E = -3.2667431000 | DE = 3.55e-15 | DW = 1.53e-20
Ground state energy = -3.266743099950662
Sweep = 0 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.018 | F = 0.9962046481 | DW = 5.23e-25
Sweep = 1 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.038 | F = 0.9970609307 | DF = 8.56e-04 | DW = 8.99e-25
Sweep = 2 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.059 | F = 0.9970609307 | DF = 4.44e-16 | DW = 6.59e-25
Sweep = 3 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.079 | F = 0.9970609307 | DF = -3.33e-16 | DW = 3.32e-25
Sweep = 4 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.101 | F = 0.9970609307 | DF = -3.33e-16 | DW = 3.88e-25
FREQ = -0.80 GF[2,2] = -2.858060 + -0.132949 i
FREQ = -0.79 GF[2,2] = -3.127639 + -0.137862 i
FREQ = -0.78 GF[2,2] = -3.410730 + -0.146788 i
FREQ = -0.77 GF[2,2] = -3.716042 + -0.159910 i
FREQ = -0.76 GF[2,2] = -4.052436 + -0.177910 i
FREQ = -0.75 GF[2,2] = -4.429247 + -0.202036 i
FREQ = -0.74 GF[2,2] = -4.862689 + -0.234242 i
FREQ = -0.73 GF[2,2] = -5.370446 + -0.277828 i
FREQ = -0.72 GF[2,2] = -5.979802 + -0.338034 i
FREQ = -0.71 GF[2,2] = -6.730787 + -0.424057 i
FREQ = -0.70 GF[2,2] = -7.689106 + -0.552665 i
FREQ = -0.69 GF[2,2] = -8.964426 + -0.757635 i
FREQ = -0.68 GF[2,2] = -10.763740 + -1.118686 i
FREQ = -0.67 GF[2,2] = -13.510429 + -1.904433 i
FREQ = -0.66 GF[2,2] = -17.418881 + -3.612921 i
FREQ = -0.65 GF[2,2] = -26.296063 + -7.892317 i
FREQ = -0.64 GF[2,2] = -44.979411 + -35.247680 i
FREQ = -0.63 GF[2,2] = 41.659891 + -56.954077 i
FREQ = -0.62 GF[2,2] = 27.132451 + -10.471813 i
FREQ = -0.61 GF[2,2] = 16.312481 + -3.861684 i
FREQ = -0.60 GF[2,2] = 11.092739 + -2.003940 i
FREQ = -0.59 GF[2,2] = 8.036382 + -1.254680 i
FREQ = -0.58 GF[2,2] = 5.972372 + -0.893065 i
FREQ = -0.57 GF[2,2] = 4.418047 + -0.708471 i
FREQ = -0.56 GF[2,2] = 3.108176 + -0.629033 i
FREQ = -0.55 GF[2,2] = 1.874834 + -0.643365 i
FREQ = -0.54 GF[2,2] = 0.501622 + -0.805649 i
FREQ = -0.53 GF[2,2] = -1.428740 + -1.392787 i
FREQ = -0.52 GF[2,2] = -5.038213 + -4.367329 i
FREQ = -0.51 GF[2,2] = 5.385607 + -16.985511 i
FREQ = -0.50 GF[2,2] = 8.132057 + -3.176944 i
FREQ = -0.49 GF[2,2] = 5.112053 + -1.122502 i
FREQ = -0.48 GF[2,2] = 3.547000 + -0.626599 i
FREQ = -0.47 GF[2,2] = 2.530196 + -0.443406 i
FREQ = -0.46 GF[2,2] = 1.745955 + -0.363108 i
FREQ = -0.45 GF[2,2] = 1.066544 + -0.329559 i
FREQ = -0.44 GF[2,2] = 0.421145 + -0.324585 i
FREQ = -0.43 GF[2,2] = -0.234970 + -0.342450 i
FREQ = -0.42 GF[2,2] = -0.955736 + -0.386035 i
FREQ = -0.41 GF[2,2] = -1.792136 + -0.464805 i
FREQ = -0.40 GF[2,2] = -2.833594 + -0.601140 i
FREQ = -0.39 GF[2,2] = -4.230434 + -0.846750 i
FREQ = -0.38 GF[2,2] = -6.289553 + -1.335939 i
FREQ = -0.37 GF[2,2] = -9.737590 + -2.501588 i
FREQ = -0.36 GF[2,2] = -16.688375 + -6.387690 i
FREQ = -0.35 GF[2,2] = -29.656382 + -31.528685 i
FREQ = -0.34 GF[2,2] = 34.225016 + -32.546412 i
FREQ = -0.33 GF[2,2] = 21.430321 + -6.498027 i
FREQ = -0.32 GF[2,2] = 14.419157 + -2.511719 i
FREQ = -0.31 GF[2,2] = 10.986939 + -1.318801 i
FREQ = -0.30 GF[2,2] = 8.980094 + -0.814240 i
FREQ = -0.29 GF[2,2] = 7.662527 + -0.555185 i
FREQ = -0.28 GF[2,2] = 6.728338 + -0.404730 i
FREQ = -0.27 GF[2,2] = 6.027647 + -0.309463 i
FREQ = -0.26 GF[2,2] = 5.481284 + -0.245307 i
FREQ = -0.25 GF[2,2] = 5.041000 + -0.199912 i
FREQ = -0.24 GF[2,2] = 4.677884 + -0.166589 i
FREQ = -0.23 GF[2,2] = 4.372155 + -0.141336 i
FREQ = -0.22 GF[2,2] = 4.110743 + -0.121720 i
FREQ = -0.21 GF[2,2] = 3.883890 + -0.106156 i
FREQ = -0.20 GF[2,2] = 3.685138 + -0.093570 i
In the SZ mode:
[3]:
import numpy as np
from pyblock2._pyscf.ao2mo import integrals as itg
from pyblock2.driver.core import DMRGDriver, SymmetryTypes
from pyscf import gto, scf, lo
BOHR = 0.52917721092
R = 1.8 * BOHR
N = 6
mol = gto.M(atom=[['H', (i * R, 0, 0)] for i in range(N)], basis="sto6g", symmetry="c1", verbose=0)
mf = scf.RHF(mol).run(conv_tol=1E-14)
mf.mo_coeff = lo.orth.lowdin(mol.intor('cint1e_ovlp_sph'))
ncas, n_elec, spin, ecore, h1e, g2e, orb_sym = itg.get_rhf_integrals(mf, ncore=0, ncas=None, g2e_symm=8)
driver = DMRGDriver(scratch="./tmp", symm_type=SymmetryTypes.SZ, n_threads=4)
driver.initialize_system(n_sites=ncas, n_elec=n_elec, spin=spin, orb_sym=orb_sym)
bond_dims = [150] * 4 + [200] * 4
noises = [1e-4] * 4 + [1e-5] * 4 + [0]
thrds = [1e-10] * 8
mpo = driver.get_qc_mpo(h1e=h1e, g2e=g2e, ecore=ecore, integral_cutoff=1E-8, iprint=1)
ket = driver.get_random_mps(tag="KET", bond_dim=150, nroots=1)
energy = driver.dmrg(mpo, ket, n_sweeps=20, bond_dims=bond_dims, noises=noises,
thrds=thrds, iprint=1)
print('Ground state energy = %20.15f' % energy)
isite = 2
mpo.const_e -= energy
eta = 0.005
dmpo = driver.get_site_mpo(op='d', site_index=isite, iprint=0) # only alpha spin
dket = driver.get_random_mps(tag="DKET", bond_dim=200, center=ket.center, target=dmpo.op.q_label + ket.info.target)
driver.multiply(dket, dmpo, ket, n_sweeps=10, bond_dims=[200], thrds=[1E-10] * 10, iprint=1)
freqs = np.arange(-0.8, -0.2, 0.01)
gfmat = np.zeros((len(freqs), ), dtype=complex)
for iw, freq in enumerate(freqs):
bra = driver.copy_mps(dket, tag="BRA") # initial guess
gfmat[iw] = driver.greens_function(bra, mpo, dmpo, ket, freq, eta, n_sweeps=6,
bra_bond_dims=[200], ket_bond_dims=[200], thrds=[1E-6] * 10, iprint=0)
print("FREQ = %8.2f GF[%d,%d] = %12.6f + %12.6f i" % (freq, isite, isite, gfmat[iw].real, gfmat[iw].imag))
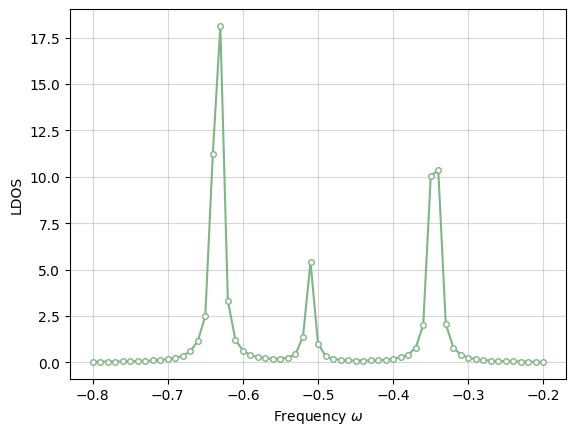
ldos = -2 / np.pi * gfmat.imag # account for both spin
import matplotlib.pyplot as plt
plt.grid(which='major', axis='both', alpha=0.5)
plt.plot(freqs, ldos, linestyle='-', marker='o', markersize=4, mfc='white', mec="#7FB685", color="#7FB685")
plt.xlabel("Frequency $\\omega$")
plt.ylabel("LDOS")
plt.show()
integral symmetrize error = 0.0
integral cutoff error = 0.0
mpo terms = 2286
Build MPO | Nsites = 6 | Nterms = 2286 | Algorithm = FastBIP | Cutoff = 1.00e-20
Site = 0 / 6 .. Mmpo = 26 DW = 0.00e+00 NNZ = 26 SPT = 0.0000 Tmvc = 0.001 T = 0.008
Site = 1 / 6 .. Mmpo = 66 DW = 0.00e+00 NNZ = 243 SPT = 0.8584 Tmvc = 0.001 T = 0.011
Site = 2 / 6 .. Mmpo = 110 DW = 0.00e+00 NNZ = 459 SPT = 0.9368 Tmvc = 0.002 T = 0.009
Site = 3 / 6 .. Mmpo = 66 DW = 0.00e+00 NNZ = 1147 SPT = 0.8420 Tmvc = 0.001 T = 0.016
Site = 4 / 6 .. Mmpo = 26 DW = 0.00e+00 NNZ = 243 SPT = 0.8584 Tmvc = 0.000 T = 0.006
Site = 5 / 6 .. Mmpo = 1 DW = 0.00e+00 NNZ = 26 SPT = 0.0000 Tmvc = 0.000 T = 0.008
Ttotal = 0.057 Tmvc-total = 0.005 MPO bond dimension = 110 MaxDW = 0.00e+00
NNZ = 2144 SIZE = 18004 SPT = 0.8809
Rank = 0 Ttotal = 0.097 MPO method = FastBipartite bond dimension = 110 NNZ = 2144 SIZE = 18004 SPT = 0.8809
Sweep = 0 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.168 | E = -3.2667431000 | DW = 1.33e-20
Sweep = 1 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.305 | E = -3.2667431000 | DE = -7.11e-15 | DW = 1.29e-20
Sweep = 2 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.432 | E = -3.2667431000 | DE = 0.00e+00 | DW = 2.12e-20
Sweep = 3 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.557 | E = -3.2667431000 | DE = 3.55e-15 | DW = 1.89e-20
Sweep = 4 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.678 | E = -3.2667431000 | DE = -1.78e-15 | DW = 1.98e-20
Sweep = 5 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.811 | E = -3.2667431000 | DE = -5.33e-15 | DW = 3.57e-20
Sweep = 6 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.935 | E = -3.2667431000 | DE = 0.00e+00 | DW = 1.87e-20
Sweep = 7 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 1.070 | E = -3.2667431000 | DE = 7.11e-15 | DW = 1.72e-20
Sweep = 8 | Direction = forward | Bond dimension = 200 | Noise = 0.00e+00 | Dav threshold = 1.00e-09
Time elapsed = 1.172 | E = -3.2667431000 | DE = -5.33e-15 | DW = 4.35e-20
Ground state energy = -3.266743099973319
Sweep = 0 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.019 | F = 0.6660221816 | DW = 9.82e-26
Sweep = 1 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.042 | F = 0.7050281723 | DF = 3.90e-02 | DW = 1.70e-24
Sweep = 2 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.063 | F = 0.7050281723 | DF = 6.66e-16 | DW = 2.63e-25
Sweep = 3 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.084 | F = 0.7050281723 | DF = 3.33e-16 | DW = 1.94e-24
Sweep = 4 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.105 | F = 0.7050281723 | DF = 1.11e-16 | DW = 8.09e-25
FREQ = -0.80 GF[2,2] = -1.429314 + -0.066472 i
FREQ = -0.79 GF[2,2] = -1.563695 + -0.068960 i
FREQ = -0.78 GF[2,2] = -1.705301 + -0.073389 i
FREQ = -0.77 GF[2,2] = -1.857857 + -0.079957 i
FREQ = -0.76 GF[2,2] = -2.026014 + -0.088950 i
FREQ = -0.75 GF[2,2] = -2.215113 + -0.101005 i
FREQ = -0.74 GF[2,2] = -2.431836 + -0.117119 i
FREQ = -0.73 GF[2,2] = -2.685052 + -0.138881 i
FREQ = -0.72 GF[2,2] = -2.989529 + -0.168989 i
FREQ = -0.71 GF[2,2] = -3.364958 + -0.212001 i
FREQ = -0.70 GF[2,2] = -3.843595 + -0.276232 i
FREQ = -0.69 GF[2,2] = -4.481702 + -0.378669 i
FREQ = -0.68 GF[2,2] = -5.379774 + -0.559234 i
FREQ = -0.67 GF[2,2] = -6.754026 + -0.952219 i
FREQ = -0.66 GF[2,2] = -8.711280 + -1.806963 i
FREQ = -0.65 GF[2,2] = -13.147719 + -3.946547 i
FREQ = -0.64 GF[2,2] = -22.488537 + -17.623137 i
FREQ = -0.63 GF[2,2] = 20.830470 + -28.478123 i
FREQ = -0.62 GF[2,2] = 13.568650 + -5.237022 i
FREQ = -0.61 GF[2,2] = 8.158524 + -1.931326 i
FREQ = -0.60 GF[2,2] = 5.546668 + -1.001994 i
FREQ = -0.59 GF[2,2] = 4.015779 + -0.627121 i
FREQ = -0.58 GF[2,2] = 2.986254 + -0.446332 i
FREQ = -0.57 GF[2,2] = 2.206705 + -0.354016 i
FREQ = -0.56 GF[2,2] = 1.553827 + -0.314387 i
FREQ = -0.55 GF[2,2] = 0.934667 + -0.321487 i
FREQ = -0.54 GF[2,2] = 0.247498 + -0.402597 i
FREQ = -0.53 GF[2,2] = -0.716559 + -0.696260 i
FREQ = -0.52 GF[2,2] = -2.517667 + -2.183247 i
FREQ = -0.51 GF[2,2] = 2.694685 + -8.495055 i
FREQ = -0.50 GF[2,2] = 4.068420 + -1.589597 i
FREQ = -0.49 GF[2,2] = 2.556421 + -0.561628 i
FREQ = -0.48 GF[2,2] = 1.776438 + -0.313770 i
FREQ = -0.47 GF[2,2] = 1.266039 + -0.222005 i
FREQ = -0.46 GF[2,2] = 0.873240 + -0.181737 i
FREQ = -0.45 GF[2,2] = 0.533170 + -0.164892 i
FREQ = -0.44 GF[2,2] = 0.210275 + -0.162307 i
FREQ = -0.43 GF[2,2] = -0.119248 + -0.171350 i
FREQ = -0.42 GF[2,2] = -0.478803 + -0.193119 i
FREQ = -0.41 GF[2,2] = -0.898305 + -0.232404 i
FREQ = -0.40 GF[2,2] = -1.418566 + -0.300549 i
FREQ = -0.39 GF[2,2] = -2.115432 + -0.423477 i
FREQ = -0.38 GF[2,2] = -3.145615 + -0.668038 i
FREQ = -0.37 GF[2,2] = -4.871226 + -1.251034 i
FREQ = -0.36 GF[2,2] = -8.345991 + -3.194131 i
FREQ = -0.35 GF[2,2] = -14.828832 + -15.765406 i
FREQ = -0.34 GF[2,2] = 17.111094 + -16.271567 i
FREQ = -0.33 GF[2,2] = 10.713170 + -3.248626 i
FREQ = -0.32 GF[2,2] = 7.207938 + -1.255671 i
FREQ = -0.31 GF[2,2] = 5.490817 + -0.659108 i
FREQ = -0.30 GF[2,2] = 4.488220 + -0.406981 i
FREQ = -0.29 GF[2,2] = 3.829440 + -0.277473 i
FREQ = -0.28 GF[2,2] = 3.362384 + -0.202273 i
FREQ = -0.27 GF[2,2] = 3.011931 + -0.154637 i
FREQ = -0.26 GF[2,2] = 2.738941 + -0.122582 i
FREQ = -0.25 GF[2,2] = 2.518611 + -0.099880 i
FREQ = -0.24 GF[2,2] = 2.336457 + -0.083188 i
FREQ = -0.23 GF[2,2] = 2.183385 + -0.070557 i
FREQ = -0.22 GF[2,2] = 2.053131 + -0.060779 i
FREQ = -0.21 GF[2,2] = 1.939693 + -0.052990 i
FREQ = -0.20 GF[2,2] = 1.840458 + -0.046715 i
Time-Dependent DMRG
Here we use real time TD-DMRG and Fast Fourier Transform (FFT) to calculate the Green’s function.
This is obtained from a Fourier transform from time domain to frequency domain:
where \(\mathrm{e}^{- \eta t}\) is a broading factor.
In the SU2 mode:
[4]:
import numpy as np
from pyblock2._pyscf.ao2mo import integrals as itg
from pyblock2.driver.core import DMRGDriver, SymmetryTypes
from pyscf import gto, scf, lo
BOHR = 0.52917721092
R = 1.8 * BOHR
N = 6
mol = gto.M(atom=[['H', (i * R, 0, 0)] for i in range(N)], basis="sto6g", symmetry="c1", verbose=0)
mf = scf.RHF(mol).run(conv_tol=1E-14)
mf.mo_coeff = lo.orth.lowdin(mol.intor('cint1e_ovlp_sph'))
ncas, n_elec, spin, ecore, h1e, g2e, orb_sym = itg.get_rhf_integrals(mf, ncore=0, ncas=None, g2e_symm=8)
driver = DMRGDriver(scratch="./tmp", symm_type=SymmetryTypes.SU2 | SymmetryTypes.CPX, n_threads=4)
driver.initialize_system(n_sites=ncas, n_elec=n_elec, spin=spin, orb_sym=orb_sym)
bond_dims = [150] * 4 + [200] * 4
noises = [1e-4] * 4 + [1e-5] * 4 + [0]
thrds = [1e-10] * 8
mpo = driver.get_qc_mpo(h1e=h1e, g2e=g2e, ecore=ecore, integral_cutoff=1E-8, iprint=1)
ket = driver.get_random_mps(tag="KET", bond_dim=150, nroots=1)
energy = driver.dmrg(mpo, ket, n_sweeps=20, bond_dims=bond_dims, noises=noises,
thrds=thrds, iprint=1)
print('Ground state energy = %20.15f' % energy)
isite = 2
mpo.const_e -= energy
eta = 0.005
dmpo = driver.get_site_mpo(op='D', site_index=isite, iprint=0)
dket = driver.get_random_mps(tag="DKET", bond_dim=200, center=ket.center, left_vacuum=dmpo.left_vacuum)
driver.multiply(dket, dmpo, ket, n_sweeps=10, bond_dims=[200], thrds=[1E-10] * 10, iprint=1)
impo = driver.get_identity_mpo()
dbra = driver.copy_mps(dket, tag='DBRA')
dt = 0.2
t = 500.0
nstep = int(t / dt)
rtgf = np.zeros((nstep, ), dtype=complex)
rtgf[0] = driver.expectation(dket, impo, dket)
for it in range(nstep - 1):
if it % (nstep // 100) == 0:
print("it = %5d (%4.1f %%)" % (it, it * 100 / nstep))
dbra = driver.td_dmrg(mpo, dbra, -dt * 1j, -dt * 1j, final_mps_tag='DBRA', hermitian=True, bond_dims=[200], iprint=0)
rtgf[it + 1] = driver.expectation(dbra, impo, dket)
def gf_fft(eta, dt, rtgf, npts):
frq = np.fft.fftfreq(npts, dt)
frq = np.fft.fftshift(frq) * 2.0 * np.pi
fftinp = -1j * rtgf * np.exp(-eta * dt * np.arange(0, npts))
return frq, np.fft.fftshift(np.fft.fft(fftinp)) * dt
frq, frq_gf = gf_fft(eta, dt, rtgf, len(rtgf))
frq_gf = frq_gf[(frq >= -0.8) & (frq < -0.2)]
frq = frq[(frq >= -0.8) & (frq < -0.2)]
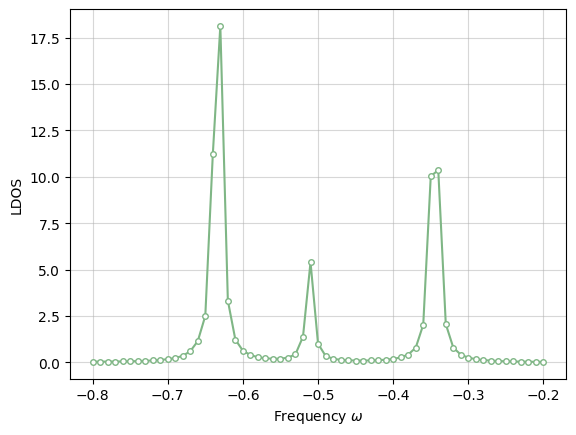
ldos = -1 / np.pi * frq_gf.imag
import matplotlib.pyplot as plt
plt.grid(which='major', axis='both', alpha=0.5)
plt.plot(frq, ldos, linestyle='-', marker='o', markersize=4, mfc='white', mec="#7FB685", color="#7FB685")
plt.xlabel("Frequency $\\omega$")
plt.ylabel("LDOS")
plt.show()
integral symmetrize error = 0.0
integral cutoff error = 0.0
mpo terms = 863
Build MPO | Nsites = 6 | Nterms = 863 | Algorithm = FastBIP | Cutoff = 1.00e-20
Site = 0 / 6 .. Mmpo = 13 DW = 0.00e+00 NNZ = 13 SPT = 0.0000 Tmvc = 0.000 T = 0.014
Site = 1 / 6 .. Mmpo = 34 DW = 0.00e+00 NNZ = 100 SPT = 0.7738 Tmvc = 0.000 T = 0.008
Site = 2 / 6 .. Mmpo = 56 DW = 0.00e+00 NNZ = 185 SPT = 0.9028 Tmvc = 0.000 T = 0.008
Site = 3 / 6 .. Mmpo = 34 DW = 0.00e+00 NNZ = 419 SPT = 0.7799 Tmvc = 0.000 T = 0.016
Site = 4 / 6 .. Mmpo = 14 DW = 0.00e+00 NNZ = 105 SPT = 0.7794 Tmvc = 0.000 T = 0.013
Site = 5 / 6 .. Mmpo = 1 DW = 0.00e+00 NNZ = 14 SPT = 0.0000 Tmvc = 0.001 T = 0.027
Ttotal = 0.087 Tmvc-total = 0.002 MPO bond dimension = 56 MaxDW = 0.00e+00
NNZ = 836 SIZE = 4753 SPT = 0.8241
Rank = 0 Ttotal = 0.190 MPO method = FastBipartite bond dimension = 56 NNZ = 836 SIZE = 4753 SPT = 0.8241
Sweep = 0 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.138 | E = -3.2667431000 | DW = 5.73e-21
Sweep = 1 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.227 | E = -3.2667431000 | DE = 4.09e-14 | DW = 1.64e-20
Sweep = 2 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.327 | E = -3.2667431000 | DE = 0.00e+00 | DW = 9.52e-21
Sweep = 3 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.428 | E = -3.2667431000 | DE = -1.78e-15 | DW = 1.55e-20
Sweep = 4 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.521 | E = -3.2667431000 | DE = -1.78e-15 | DW = 6.12e-21
Sweep = 5 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.634 | E = -3.2667431000 | DE = -3.55e-15 | DW = 2.47e-20
Sweep = 6 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.781 | E = -3.2667431000 | DE = 7.11e-15 | DW = 7.01e-21
Sweep = 7 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.876 | E = -3.2667431000 | DE = 1.78e-15 | DW = 1.12e-20
Sweep = 8 | Direction = forward | Bond dimension = 200 | Noise = 0.00e+00 | Dav threshold = 1.00e-09
Time elapsed = 0.997 | E = -3.2667431000 | DE = 1.78e-15 | DW = 1.93e-20
Ground state energy = -3.266743099951065
Sweep = 0 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.057 | F = (0.9960879032,0.0000000000) | DW = 3.05e-25
Sweep = 1 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.120 | F = (0.9970594762,0.0000000000) | DF = (9.72e-04,0.00e+00) | DW = 9.73e-25
Sweep = 2 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.168 | F = (0.9970594762,0.0000000000) | DF = (4.44e-16,0.00e+00) | DW = 1.57e-25
Sweep = 3 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.213 | F = (0.9970594762,0.0000000000) | DF = (-5.55e-16,0.00e+00) | DW = 3.36e-25
Sweep = 4 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.262 | F = (0.9970594762,0.0000000000) | DF = (2.22e-16,0.00e+00) | DW = 1.04e-24
it = 0 ( 0.0 %)
it = 25 ( 1.0 %)
it = 50 ( 2.0 %)
it = 75 ( 3.0 %)
it = 100 ( 4.0 %)
it = 125 ( 5.0 %)
it = 150 ( 6.0 %)
it = 175 ( 7.0 %)
it = 200 ( 8.0 %)
it = 225 ( 9.0 %)
it = 250 (10.0 %)
it = 275 (11.0 %)
it = 300 (12.0 %)
it = 325 (13.0 %)
it = 350 (14.0 %)
it = 375 (15.0 %)
it = 400 (16.0 %)
it = 425 (17.0 %)
it = 450 (18.0 %)
it = 475 (19.0 %)
it = 500 (20.0 %)
it = 525 (21.0 %)
it = 550 (22.0 %)
it = 575 (23.0 %)
it = 600 (24.0 %)
it = 625 (25.0 %)
it = 650 (26.0 %)
it = 675 (27.0 %)
it = 700 (28.0 %)
it = 725 (29.0 %)
it = 750 (30.0 %)
it = 775 (31.0 %)
it = 800 (32.0 %)
it = 825 (33.0 %)
it = 850 (34.0 %)
it = 875 (35.0 %)
it = 900 (36.0 %)
it = 925 (37.0 %)
it = 950 (38.0 %)
it = 975 (39.0 %)
it = 1000 (40.0 %)
it = 1025 (41.0 %)
it = 1050 (42.0 %)
it = 1075 (43.0 %)
it = 1100 (44.0 %)
it = 1125 (45.0 %)
it = 1150 (46.0 %)
it = 1175 (47.0 %)
it = 1200 (48.0 %)
it = 1225 (49.0 %)
it = 1250 (50.0 %)
it = 1275 (51.0 %)
it = 1300 (52.0 %)
it = 1325 (53.0 %)
it = 1350 (54.0 %)
it = 1375 (55.0 %)
it = 1400 (56.0 %)
it = 1425 (57.0 %)
it = 1450 (58.0 %)
it = 1475 (59.0 %)
it = 1500 (60.0 %)
it = 1525 (61.0 %)
it = 1550 (62.0 %)
it = 1575 (63.0 %)
it = 1600 (64.0 %)
it = 1625 (65.0 %)
it = 1650 (66.0 %)
it = 1675 (67.0 %)
it = 1700 (68.0 %)
it = 1725 (69.0 %)
it = 1750 (70.0 %)
it = 1775 (71.0 %)
it = 1800 (72.0 %)
it = 1825 (73.0 %)
it = 1850 (74.0 %)
it = 1875 (75.0 %)
it = 1900 (76.0 %)
it = 1925 (77.0 %)
it = 1950 (78.0 %)
it = 1975 (79.0 %)
it = 2000 (80.0 %)
it = 2025 (81.0 %)
it = 2050 (82.0 %)
it = 2075 (83.0 %)
it = 2100 (84.0 %)
it = 2125 (85.0 %)
it = 2150 (86.0 %)
it = 2175 (87.0 %)
it = 2200 (88.0 %)
it = 2225 (89.0 %)
it = 2250 (90.0 %)
it = 2275 (91.0 %)
it = 2300 (92.0 %)
it = 2325 (93.0 %)
it = 2350 (94.0 %)
it = 2375 (95.0 %)
it = 2400 (96.0 %)
it = 2425 (97.0 %)
it = 2450 (98.0 %)
it = 2475 (99.0 %)
In the SZ mode:
[5]:
import numpy as np
from pyblock2._pyscf.ao2mo import integrals as itg
from pyblock2.driver.core import DMRGDriver, SymmetryTypes
from pyscf import gto, scf, lo
BOHR = 0.52917721092
R = 1.8 * BOHR
N = 6
mol = gto.M(atom=[['H', (i * R, 0, 0)] for i in range(N)], basis="sto6g", symmetry="c1", verbose=0)
mf = scf.RHF(mol).run(conv_tol=1E-14)
mf.mo_coeff = lo.orth.lowdin(mol.intor('cint1e_ovlp_sph'))
ncas, n_elec, spin, ecore, h1e, g2e, orb_sym = itg.get_rhf_integrals(mf, ncore=0, ncas=None, g2e_symm=8)
driver = DMRGDriver(scratch="./tmp", symm_type=SymmetryTypes.SZ | SymmetryTypes.CPX, n_threads=4)
driver.initialize_system(n_sites=ncas, n_elec=n_elec, spin=spin, orb_sym=orb_sym)
bond_dims = [150] * 4 + [200] * 4
noises = [1e-4] * 4 + [1e-5] * 4 + [0]
thrds = [1e-10] * 8
mpo = driver.get_qc_mpo(h1e=h1e, g2e=g2e, ecore=ecore, integral_cutoff=1E-8, iprint=1)
ket = driver.get_random_mps(tag="KET", bond_dim=150, nroots=1)
energy = driver.dmrg(mpo, ket, n_sweeps=20, bond_dims=bond_dims, noises=noises,
thrds=thrds, iprint=1)
print('Ground state energy = %20.15f' % energy)
isite = 2
mpo.const_e -= energy
eta = 0.005
dmpo = driver.get_site_mpo(op='d', site_index=isite, iprint=0) # only alpha spin
dket = driver.get_random_mps(tag="DKET", bond_dim=200, center=ket.center, target=dmpo.op.q_label + ket.info.target)
driver.multiply(dket, dmpo, ket, n_sweeps=10, bond_dims=[200], thrds=[1E-10] * 10, iprint=1)
impo = driver.get_identity_mpo()
dbra = driver.copy_mps(dket, tag='DBRA')
dt = 0.2
t = 500.0
nstep = int(t / dt)
rtgf = np.zeros((nstep, ), dtype=complex)
rtgf[0] = driver.expectation(dket, impo, dket)
for it in range(nstep - 1):
if it % (nstep // 100) == 0:
print("it = %5d (%4.1f %%)" % (it, it * 100 / nstep))
dbra = driver.td_dmrg(mpo, dbra, -dt * 1j, -dt * 1j, final_mps_tag='DBRA', hermitian=True, bond_dims=[200], iprint=0)
rtgf[it + 1] = driver.expectation(dbra, impo, dket)
def gf_fft(eta, dt, rtgf, npts):
frq = np.fft.fftfreq(npts, dt)
frq = np.fft.fftshift(frq) * 2.0 * np.pi
fftinp = -1j * rtgf * np.exp(-eta * dt * np.arange(0, npts))
return frq, np.fft.fftshift(np.fft.fft(fftinp)) * dt
frq, frq_gf = gf_fft(eta, dt, rtgf, len(rtgf))
frq_gf = frq_gf[(frq >= -0.8) & (frq < -0.2)]
frq = frq[(frq >= -0.8) & (frq < -0.2)]
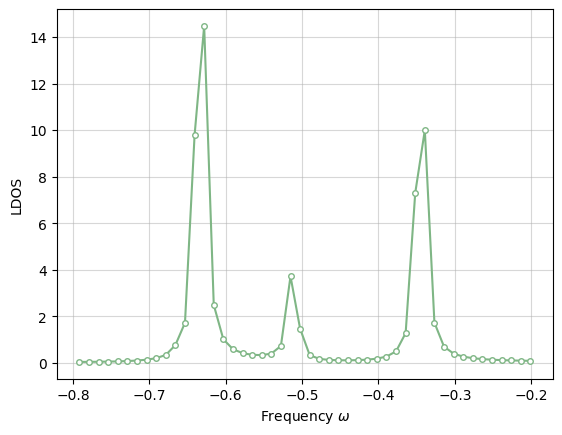
ldos = -2 / np.pi * frq_gf.imag
import matplotlib.pyplot as plt
plt.grid(which='major', axis='both', alpha=0.5)
plt.plot(frq, ldos, linestyle='-', marker='o', markersize=4, mfc='white', mec="#7FB685", color="#7FB685")
plt.xlabel("Frequency $\\omega$")
plt.ylabel("LDOS")
plt.show()
integral symmetrize error = 0.0
integral cutoff error = 0.0
mpo terms = 2286
Build MPO | Nsites = 6 | Nterms = 2286 | Algorithm = FastBIP | Cutoff = 1.00e-20
Site = 0 / 6 .. Mmpo = 26 DW = 0.00e+00 NNZ = 26 SPT = 0.0000 Tmvc = 0.001 T = 0.016
Site = 1 / 6 .. Mmpo = 66 DW = 0.00e+00 NNZ = 243 SPT = 0.8584 Tmvc = 0.001 T = 0.016
Site = 2 / 6 .. Mmpo = 110 DW = 0.00e+00 NNZ = 459 SPT = 0.9368 Tmvc = 0.001 T = 0.014
Site = 3 / 6 .. Mmpo = 66 DW = 0.00e+00 NNZ = 1147 SPT = 0.8420 Tmvc = 0.001 T = 0.013
Site = 4 / 6 .. Mmpo = 26 DW = 0.00e+00 NNZ = 243 SPT = 0.8584 Tmvc = 0.000 T = 0.004
Site = 5 / 6 .. Mmpo = 1 DW = 0.00e+00 NNZ = 26 SPT = 0.0000 Tmvc = 0.000 T = 0.003
Ttotal = 0.066 Tmvc-total = 0.004 MPO bond dimension = 110 MaxDW = 0.00e+00
NNZ = 2144 SIZE = 18004 SPT = 0.8809
Rank = 0 Ttotal = 0.124 MPO method = FastBipartite bond dimension = 110 NNZ = 2144 SIZE = 18004 SPT = 0.8809
Sweep = 0 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.230 | E = -3.2667431000 | DW = 7.12e-17
Sweep = 1 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.413 | E = -3.2667431000 | DE = -1.78e-15 | DW = 6.71e-17
Sweep = 2 | Direction = forward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.563 | E = -3.2667431000 | DE = 3.55e-15 | DW = 6.86e-17
Sweep = 3 | Direction = backward | Bond dimension = 150 | Noise = 1.00e-04 | Dav threshold = 1.00e-10
Time elapsed = 0.770 | E = -3.2667431000 | DE = 0.00e+00 | DW = 7.22e-17
Sweep = 4 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 0.951 | E = -3.2667431000 | DE = -3.55e-15 | DW = 1.68e-20
Sweep = 5 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 1.109 | E = -3.2667431000 | DE = 0.00e+00 | DW = 2.60e-20
Sweep = 6 | Direction = forward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 1.261 | E = -3.2667431000 | DE = 0.00e+00 | DW = 1.87e-20
Sweep = 7 | Direction = backward | Bond dimension = 200 | Noise = 1.00e-05 | Dav threshold = 1.00e-10
Time elapsed = 1.415 | E = -3.2667431000 | DE = 0.00e+00 | DW = 3.66e-20
Sweep = 8 | Direction = forward | Bond dimension = 200 | Noise = 0.00e+00 | Dav threshold = 1.00e-09
Time elapsed = 1.526 | E = -3.2667431000 | DE = -1.78e-15 | DW = 5.13e-20
Ground state energy = -3.266743099950349
Sweep = 0 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.022 | F = (0.6266622731,0.0000000000) | DW = 7.22e-25
Sweep = 1 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.051 | F = (0.7050283557,0.0000000000) | DF = (7.84e-02,0.00e+00) | DW = 9.91e-25
Sweep = 2 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.076 | F = (0.7050283557,0.0000000000) | DF = (4.44e-16,0.00e+00) | DW = 7.16e-25
Sweep = 3 | Direction = forward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.112 | F = (0.7050283557,0.0000000000) | DF = (-1.11e-16,0.00e+00) | DW = 1.77e-24
Sweep = 4 | Direction = backward | BRA bond dimension = 200 | Noise = 0.00e+00
Time elapsed = 0.148 | F = (0.7050283557,0.0000000000) | DF = (-1.11e-16,0.00e+00) | DW = 7.19e-25
it = 0 ( 0.0 %)
it = 25 ( 1.0 %)
it = 50 ( 2.0 %)
it = 75 ( 3.0 %)
it = 100 ( 4.0 %)
it = 125 ( 5.0 %)
it = 150 ( 6.0 %)
it = 175 ( 7.0 %)
it = 200 ( 8.0 %)
it = 225 ( 9.0 %)
it = 250 (10.0 %)
it = 275 (11.0 %)
it = 300 (12.0 %)
it = 325 (13.0 %)
it = 350 (14.0 %)
it = 375 (15.0 %)
it = 400 (16.0 %)
it = 425 (17.0 %)
it = 450 (18.0 %)
it = 475 (19.0 %)
it = 500 (20.0 %)
it = 525 (21.0 %)
it = 550 (22.0 %)
it = 575 (23.0 %)
it = 600 (24.0 %)
it = 625 (25.0 %)
it = 650 (26.0 %)
it = 675 (27.0 %)
it = 700 (28.0 %)
it = 725 (29.0 %)
it = 750 (30.0 %)
it = 775 (31.0 %)
it = 800 (32.0 %)
it = 825 (33.0 %)
it = 850 (34.0 %)
it = 875 (35.0 %)
it = 900 (36.0 %)
it = 925 (37.0 %)
it = 950 (38.0 %)
it = 975 (39.0 %)
it = 1000 (40.0 %)
it = 1025 (41.0 %)
it = 1050 (42.0 %)
it = 1075 (43.0 %)
it = 1100 (44.0 %)
it = 1125 (45.0 %)
it = 1150 (46.0 %)
it = 1175 (47.0 %)
it = 1200 (48.0 %)
it = 1225 (49.0 %)
it = 1250 (50.0 %)
it = 1275 (51.0 %)
it = 1300 (52.0 %)
it = 1325 (53.0 %)
it = 1350 (54.0 %)
it = 1375 (55.0 %)
it = 1400 (56.0 %)
it = 1425 (57.0 %)
it = 1450 (58.0 %)
it = 1475 (59.0 %)
it = 1500 (60.0 %)
it = 1525 (61.0 %)
it = 1550 (62.0 %)
it = 1575 (63.0 %)
it = 1600 (64.0 %)
it = 1625 (65.0 %)
it = 1650 (66.0 %)
it = 1675 (67.0 %)
it = 1700 (68.0 %)
it = 1725 (69.0 %)
it = 1750 (70.0 %)
it = 1775 (71.0 %)
it = 1800 (72.0 %)
it = 1825 (73.0 %)
it = 1850 (74.0 %)
it = 1875 (75.0 %)
it = 1900 (76.0 %)
it = 1925 (77.0 %)
it = 1950 (78.0 %)
it = 1975 (79.0 %)
it = 2000 (80.0 %)
it = 2025 (81.0 %)
it = 2050 (82.0 %)
it = 2075 (83.0 %)
it = 2100 (84.0 %)
it = 2125 (85.0 %)
it = 2150 (86.0 %)
it = 2175 (87.0 %)
it = 2200 (88.0 %)
it = 2225 (89.0 %)
it = 2250 (90.0 %)
it = 2275 (91.0 %)
it = 2300 (92.0 %)
it = 2325 (93.0 %)
it = 2350 (94.0 %)
it = 2375 (95.0 %)
it = 2400 (96.0 %)
it = 2425 (97.0 %)
it = 2450 (98.0 %)
it = 2475 (99.0 %)